ACM
July 22, 2021

二分图

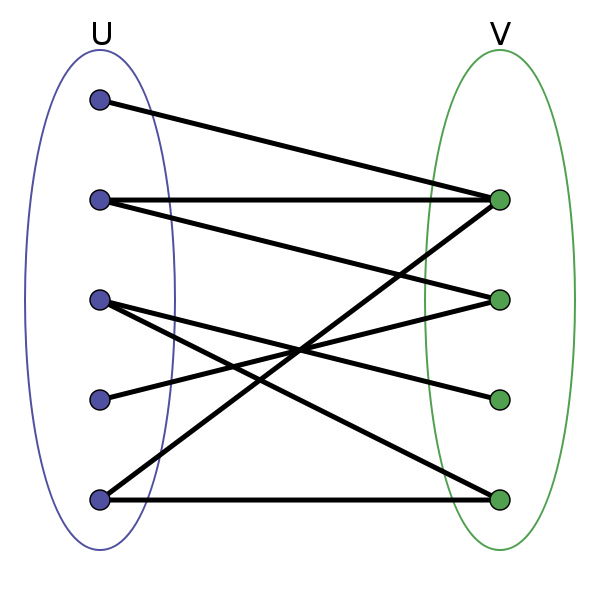
二分图

简介

二分图又称作二部图，是图论中的一种特殊模型。 设 G = (V, E) 是一个无向图，如果：

则称图 G 为一个二分图。

简单来说，把一个图的顶点划分为两个不相交子集 ，使得每一条边都分别连接两个集合中的顶点。如果存在这样的划分，则此图为一个二分图。

性质

判定：染色法

思路

根据二分图只有偶环的性质，我们可以使用 DFS 或者 BFS 来遍历这张图。如果发现了奇环，那么就不是二分图，否则是。

任意选取一个点，将其颜色染为红色，将与其相邻的节点染为绿色，接着把与绿色相邻的节点染为红色……直到出现两个相邻的节点为同一颜色：不是二分图；或成功将所有节点染色：是二分图。

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#define _CRTSECURE_nOWARnInGS
#pragma warning(disable:4996)
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <cctype>
#include <algorithm>
#include <iostream>
#include <queue>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <list>
using namespace std;

const int MAXN = 100015, MAXM = 500015;

int T, n, m;		//n 个节点，m 条边
int cnt;
int front[MAXM];

struct EDGE
{
	int to, next, w;
};

EDGE edge[MAXM];

void Init()
{
	memset(front, 0, sizeof(front));
	cnt = 0;
}

void add_edge(int u, int v, int w)
{
	++cnt;
	edge[cnt].to = v;
	edge[cnt].w = w;
	edge[cnt].next = front[u];
	front[u] = cnt;
}

int color[MAXN];		//color[i]=0,1,2 表i节点不涂颜色、涂白色、涂黑色

bool bipartite(int u)	//判断无向图是否可二分
{
	for (int i = front[u]; i; i = edge[i].next)	//枚举结点
	{
		int v = edge[i].to;			//相邻节点
		if (color[v] == color[u])		//若两结点颜色相同，无法二分
			return 0;
		if (!color[v])			//若结点没涂颜色
		{
			color[v] = 3 - color[u];		//改变结点颜色，使v的颜色与u的颜色对立
			if (!bipartite(v))		//若点v不满足二分图话，则无法二分
				return 0;
		}
	}
	return 1;
}


int main()
{
	Init();
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= m; i++)
	{
		int u, v;
		scanf("%d%d", &u, &v);
		add_edge(u, v, 1);
		add_edge(v, u, 1);	//双向边
	}
	memset(color, 0, sizeof(color));
	color[1] = 1;
	if (bipartite(1)) printf("YES\n");
	else printf("NO\n");

	return 0;

}

相关概念

匹配

在给定一个二分图 G，在 G 的一个子图 M 中，若 M 的边集中的任意两条边都不依附于同一个顶点，则称 M 是一个匹配。

简单来说，匹配就是一个二分图中边的集合，其中任意两条边都没有公共顶点。

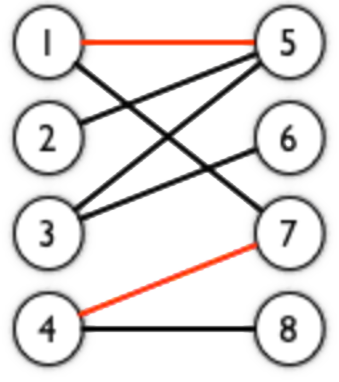
上图中红色边连接的 1 - 5 和 4 - 7 就是两个匹配。

最大匹配

给定二分图 G 中的所有匹配，所含匹配边数最多的匹配，称为这个图的最大匹配，选择最大匹配的问题即为图的最大匹配问题

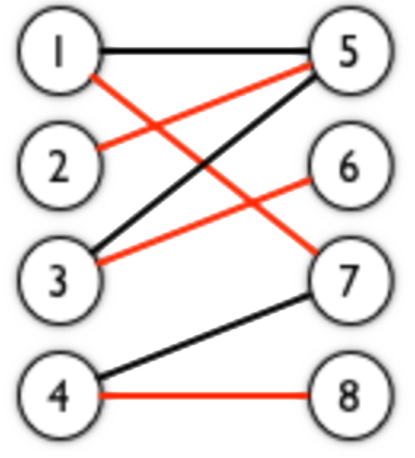
如图，红边就是一个最大匹配

即：在不存在一个顶点连接多条边的情况下，连接尽量多的边

完全匹配

一个匹配中，图中每个顶点都与图中某条边相关联，则称此匹配为完全匹配，即一个图的某个匹配中，所有的顶点都是匹配点，就是一个完全匹配。

显然，由于完全匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突，因此完全匹配一定是最大匹配。但要注意的是，并非每个图都存在完全匹配。

简单来说，对于一个二分图，左右点集数量不一定相同，左点集中的每一个点都与右点集的一个点匹配，或者右点集中的每一个点都与左点集的一个点匹配。（两个点集其中之一满足一对一即可）

完美匹配

对于一个二分图，左点集与右点集的点数相同，若存在一个匹配，包含左点集、右点集的所有顶点，则称为完美匹配。

简单来说，对于一个二分图，左右点集数量相同，左点集中的每一个点都与右点集的一个点匹配，并且右点集中的每一个点都与左点集的一个点匹配。（两个点集都要满足一对一）

应用

无权重最大匹配：匈牙利算法

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <cctype>
#include <algorithm>
#include <iostream>
#include <queue>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <list>
using namespace std;

const int MAXN = 301;

int p, n;		//A 集合有 p 个元素，B 集合有 n 个元素
int ans;		//无权重最大匹配数
int mp[MAXN][MAXN];		//mp[x][y]：x、y 之间有一条边（无需建双向边）
int vis[MAXN], a[MAXN];

bool dfs(int x)
{
	for (int i = 1; i <= n; i++)
	{
		if (!vis[i] && mp[x][i])
		{
			vis[i] = 1;
			if (a[i] == 0 || dfs(a[i]))
			{
				a[i] = x;
				return 1;
			}
		}
	}
	return 0;
}

int main()
{
	ans = 0;
	scanf("%d%d", &p, &n);
	memset(a, 0, sizeof(a));
	memset(mp, 0, sizeof(mp));
	/*	根据题目意思灵活读图
	for (int i = 1; i <= p; i++)
	{
		int a;
		scanf("%d", &a);
		for (int j = 1; j <= a; j++)
		{
			int x;
			scanf("%d", &x);
			mp[i][x] = 1;
		}
	}
	*/
	for (int i = 1; i <= p; i++)
	{
		memset(vis, 0, sizeof(vis));
		if (dfs(i)) ans++;
	}

	printf("%d", ans);


	return 0;

}

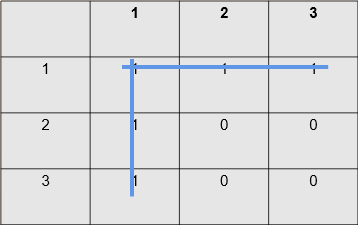
最小点覆盖数

在一个二分图中，每次选一个点覆盖住他所在的一行或者一列，选取最少的点可以把所有的边覆盖， 点的最少个数就是最小点覆盖。

在关系矩阵中，一次将一行/一列的 1 变为 0，求最少变化次数将所有 1 变为 0。

最大独立集

最小边覆盖

最大带权匹配：KM 算法

时间复杂度 · $O(n^{3})$​

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
template <typename T>
struct hungarian			// km
{
	int n;
	vector<int> matchx;		// 左集合对应的匹配点
	vector<int> matchy;		// 右集合对应的匹配点
	vector<int> pre;		// 连接右集合的左点
	vector<bool> visx;		// 拜访数组 左
	vector<bool> visy;		// 拜访数组 右
	vector<T> lx;
	vector<T> ly;
	vector<vector<T> > g;
	vector<T> slack;
	T inf;
	T res;
	queue<int> q;
	int org_n;
	int org_m;

	hungarian(int _n, int _m)
	{
		org_n = _n;
		org_m = _m;
		n = max(_n, _m);
		inf = numeric_limits<T>::max();
		res = 0;
		g = vector<vector<T> >(n, vector<T>(n));
		matchx = vector<int>(n, -1);
		matchy = vector<int>(n, -1);
		pre = vector<int>(n);
		visx = vector<bool>(n);
		visy = vector<bool>(n);
		lx = vector<T>(n, -inf);
		ly = vector<T>(n);
		slack = vector<T>(n);
	}

	void addEdge(int u, int v, int w)
	{
		g[u][v] = max(w, 0);		// 负值还不如不匹配 因此设为0不影响
	}

	bool check(int v)
	{
		visy[v] = true;
		if (matchy[v] != -1)
		{
			q.push(matchy[v]);
			visx[matchy[v]] = true;		// in S
			return false;
		}
		// 找到新的未匹配点 更新匹配点 pre 数组记录着"非匹配边"上与之相连的点
		while (v != -1)
		{
			matchy[v] = pre[v];
			swap(v, matchx[pre[v]]);
		}
		return true;
	}

	void bfs(int i)
	{
		while (!q.empty())
		{
			q.pop();
		}
		q.push(i);
		visx[i] = true;
		while (true)
		{
			while (!q.empty())
			{
				int u = q.front();
				q.pop();
				for (int v = 0; v < n; v++)
				{
					if (!visy[v])
					{
						T delta = lx[u] + ly[v] - g[u][v];
						if (slack[v] >= delta)
						{
							pre[v] = u;
							if (delta)
							{
								slack[v] = delta;
							}
							else if (check(v))		// delta=0 代表有机会加入相等子图 找增广路
							{
								return;		// 找到就return 重建交错树
							}
						}
					}
				}
			}
			// 没有增广路 修改顶标
			T a = inf;
			for (int j = 0; j < n; j++)
			{
				if (!visy[j])
				{
					a = min(a, slack[j]);
				}
			}
			for (int j = 0; j < n; j++)
			{
				if (visx[j])		// S
				{
					lx[j] -= a;
				}
				if (visy[j])		// T
				{
					ly[j] += a;
				}
				else				// T'
				{
					slack[j] -= a;
				}
			}
			for (int j = 0; j < n; j++) {
				if (!visy[j] && slack[j] == 0 && check(j)) {
					return;
				}
			}
		}
	}

	void solve()
	{
		// 初始顶标
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < n; j++)
			{
				lx[i] = max(lx[i], g[i][j]);
			}
		}

		for (int i = 0; i < n; i++)
		{
			fill(slack.begin(), slack.end(), inf);
			fill(visx.begin(), visx.end(), false);
			fill(visy.begin(), visy.end(), false);
			bfs(i);
		}

		// custom
		for (int i = 0; i < n; i++)
		{
			if (g[i][matchx[i]] > 0)
			{
				res += g[i][matchx[i]];
			}
			else
			{
				matchx[i] = -1;
			}
		}
		cout << res << "\n";
		for (int i = 0; i < org_n; i++)
		{
			cout << matchx[i] + 1 << " ";
		}
		cout << "\n";
	}
};

食用方法见下

UniversalOJ 80 · 二分图最大权匹配

Description

从前一个和谐的班级，有 $n_{l}$​ 个是男生，有 $n_{r}$​ 个是女生。编号分别为 $1, \ …, \ n_{l}$​ 和 $1, \ …, \ n_{r}$。

有若干个这样的条件：第 v 个男生和第 u 个女生愿意结为配偶，且结为配偶后幸福程度为 w。

请问这个班级里幸福程度之和最大是多少？

$1 \ \leq \ n_{l}, \ n_{r} \ \leq \ 400$，$1 \ \leq \ m \ \leq \ 160000$，$1 \ \leq \ w \ \leq \ 10^{9}$。

Input

第一行三个正整数，$n_{l}, \ n_{r}, \ m$。

接下来 m 行，每行三个整数 v, u, w 表示第 v 个男生和第 u 个女生愿意结为配偶，且幸福程度为 w。保证 $1 \ \leq \ v \ \leq \ n_{l}$，$1 \ \leq \ u \ \leq \ n_{r}$，保证同一对 v, u 不会出现两次。

Output

第一行一个整数，表示幸福程度之和的最大值。

接下来一行 $n_{l}$ 个整数，描述一组最优方案。第 v 个整数表示 v 号男生的配偶的编号。如果 v 号男生没配偶请输出 0。

Sample Input
1
2
3
4
2 2 3
1 1 100
1 2 1
2 1 1
Sample Output
1
2
100
1 0
Accpted Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <cctype>
#include <algorithm>
#include <iostream>
#include <queue>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <list>
using namespace std;

template <typename T>
struct hungarian		// km
{
	int n;
	vector<int> matchx;
	vector<int> matchy;
	vector<int> pre;
	vector<bool> visx;
	vector<bool> visy;
	vector<T> lx;
	vector<T> ly;
	vector<vector<T> > g;
	vector<T> slack;
	T inf;
	T res;
	queue<int> q;
	int org_n;
	int org_m;

	hungarian(int _n, int _m)
	{
		org_n = _n;
		org_m = _m;
		n = max(_n, _m);
		inf = numeric_limits<T>::max();
		res = 0;
		g = vector<vector<T> >(n, vector<T>(n));
		matchx = vector<int>(n, -1);
		matchy = vector<int>(n, -1);
		pre = vector<int>(n);
		visx = vector<bool>(n);
		visy = vector<bool>(n);
		lx = vector<T>(n, -inf);
		ly = vector<T>(n);
		slack = vector<T>(n);
	}

	void addEdge(int u, int v, int w)
	{
		g[u][v] = max(w, 0);		// 负值还不如不匹配 因此设为0不影响
	}

	bool check(int v)
	{
		visy[v] = true;
		if (matchy[v] != -1)
		{
			q.push(matchy[v]);
			visx[matchy[v]] = true;
			return false;
		}
		while (v != -1)
		{
			matchy[v] = pre[v];
			swap(v, matchx[pre[v]]);
		}
		return true;
	}

	void bfs(int i)
	{
		while (!q.empty())
		{
			q.pop();
		}
		q.push(i);
		visx[i] = true;
		while (true)
		{
			while (!q.empty())
			{
				int u = q.front();
				q.pop();
				for (int v = 0; v < n; v++)
				{
					if (!visy[v])
					{
						T delta = lx[u] + ly[v] - g[u][v];
						if (slack[v] >= delta)
						{
							pre[v] = u;
							if (delta)
							{
								slack[v] = delta;
							}
							else if (check(v))
							{
								return;
							}
						}
					}
				}
			}
			// 没有增广路 修改顶标
			T a = inf;
			for (int j = 0; j < n; j++)
			{
				if (!visy[j])
				{
					a = min(a, slack[j]);
				}
			}
			for (int j = 0; j < n; j++)
			{
				if (visx[j])		// S
				{
					lx[j] -= a;
				}
				if (visy[j])		// T
				{
					ly[j] += a;
				}
				else				// T'
				{
					slack[j] -= a;
				}
			}
			for (int j = 0; j < n; j++)
			{
				if (!visy[j] && slack[j] == 0 && check(j))
				{
					return;
				}
			}
		}
	}

	void solve()
	{
		// 初始顶标
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < n; j++)
			{
				lx[i] = max(lx[i], g[i][j]);
			}
		}

		for (int i = 0; i < n; i++)
		{
			fill(slack.begin(), slack.end(), inf);
			fill(visx.begin(), visx.end(), false);
			fill(visy.begin(), visy.end(), false);
			bfs(i);
		}

		// custom
		for (int i = 0; i < n; i++)
		{
			if (g[i][matchx[i]] > 0)
			{
				res += g[i][matchx[i]];
			}
			else
			{
				matchx[i] = -1;
			}
		}
		cout << res << "\n";
		for (int i = 0; i < org_n; i++)
		{
			cout << matchx[i] + 1 << " ";
		}
		cout << "\n";
	}
};

int main()
{
	ios::sync_with_stdio(0), cin.tie(0);
	int n, m, e;		//A 集合 n 个数，B 集合 m 个数，e 条关系
	cin >> n >> m >> e;

	hungarian<long long> solver(n, m);

	int u, v, w;
	for (int i = 0; i < e; i++)
	{
		cin >> u >> v >> w;
		u--, v--;
		solver.addEdge(u, v, w);
	}
	solver.solve();


	return 0;

}

About this Post

This post is written by OwlllOvO, licensed under CC BY-NC 4.0.

#C++#二分图