ACM

May 2, 2021

DP

基础 DP

最长公共子串

特点

连续

思路

动态转移方程

if (a[i] == b[j]) dp[i][j] = dp[i-1][j-1] + 1;

else dp[i][j] = 0;

模板

#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<iostream>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<list>
using namespace std;
#define INF 0x7fffffff

int n, m;
char a[10001], b[10001];
int dp[10001][10001];
int maxn;

int main()
{
	scanf("%s", a + 1);
	scanf("%s", b + 1);
	int n = strlen(a + 1);
	int m = strlen(b + 1);
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			if (a[i] == b[j]) dp[i][j] = dp[i - 1][j - 1] + 1;
			maxn = max(maxn, dp[i][j]);
		}
	}
	printf("%d", maxn);

	return 0;

}

最长公共子序列

特点

可以不连续

动态转移方程

if (a[i] == b[j]) dp[i][j] = dp[i-1][j-1] + 1;
dp[i][j] = max(dp[i][j], dp[i-1][j], dp[i][j-1]);

模板

#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<iostream>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<list>
using namespace std;
#define INF 0x7fffffff

int n, m;
int a[10001], b[10001];
int dp[10001][10001];

bool cmp(int x, int y)
{
	return x > y;
}

int max1(int x, int y, int z)
{
	int t[4] = { 0, x, y, z };
	sort(t + 1, t + 4, cmp);
	return t[1];
}

int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
	for (int i = 1; i <= m; i++) scanf("%d", &b[i]);
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			if (a[i] == b[j]) dp[i][j] = dp[i - 1][j - 1] + 1;
			dp[i][j] = max1(dp[i][j], dp[i - 1][j], dp[i][j - 1]);
		}
	}
	printf("%d", dp[n][m]);

	return 0;

}

01 背包

简介

已知条件有第 i 个物品的重量 w[i]，价值 v[i]，以及背包的总容量 W。

特点

有多样物品

每样物品只有一件
每件物品只有 取 或 不取 两种状态

思路

dp[i][j]：在只能取前 i 件物品的情况下，容量为 j 的背包能取的最大价值

假设当前已经处理好了前 i - 1 个物品的所有状态，那么对于第 i 个物品，有取或不取两种选择

当其不放入背包时，背包的剩余容量不变，背包中物品的总价值也不变，故这种情况的最大价值为 f[i-1][j]
当其放入背包时，背包的剩余容量会减小，背包中物品的总价值会增大，故这种情况的最大价值为 f[i-1][j-w[i]] + v[i]。

动态转移方程：dp[i][j] = max(dp[i-1][j], dp[i-1][j - w[i]] + v[i])

模板

1
2
3

for (int i = 1; i <= n; i++)
  for (int j = w[i]; j <= W; j++)
    dp[i][j] = max(dp[i-1][j], dp[i-1][j - w[i]] + v[i]);

优化

可以发现，第 i 次循环时的 dp 数组只受第 i - 1 层的影响，因此可以去掉第一维

但是若 j 从前往后便利，则会在同一层将之后需要用到的数据覆盖掉，相当于可以多次将物品 i 多次放入背包（这就是完全背包的解法），因此要从后往前遍历。

动态转移方程：dp[j] = max(dp[j], dp[j - w[i]] + v[i])

模板

1
2
3

for (int i = 1; i <= n; i++)
  for (int j = W; j >= w[i]; j--)
    dp[j] = max(dp[j], dp[j - w[i]] + v[i]);

完全背包

简介

已知条件有第 i 个物品的重量 w[i]，价值 v[i]，以及背包的总容量 W。

特点

有多样物品

每样物品有无数件
每件物品只有 取 或 不取 两种状态

思路

dp[i][j]：在只能取前 i 件物品的情况下，容量为 j 的背包能取的最大价值

遍历时对于 取 的状态，在同一层中计算，因此 j 将遍历到第 i 件物品的倍数，相当于对这件物品多次取

若 j 从后往前遍历，会出现同一层中需要用到的数据还未计算的情况，因此需从前往后遍历。

动态转移方程：dp[i][j] = max(dp[i-1][j], dp[i][j - w[i]] + v[i])

模板

1
2
3

dpor (int i = 1; i <= n; i++)
  dpor (int j = w[i]; j <= W; j++)
    dp[i][j] = max(dp[i-1][j], dp[i][j - w[i]] + v[i]);

优化

跟 01 背包的优化思路一样，可以去除一层数组

dp[j] = max(dp[j], dp[j - w[i]] + v[i])

模板

1
2
3

dpor (int i = 1; i <= n; i++)
  dpor (int j = w[i]; j <= W; j++)
    dp[j] = max(dp[j], dp[j - w[i]] + v[i])

多重背包

简介

已知条件有第 i 个物品的重量 w[i]，价值 v[i]，以及背包的总容量 W。

特点

有多样物品

每样物品有 1 件 或 k 件
每件物品只有 取 或 不取 两种状态

思路

把 “每种物品有 k_i 件” 等价转换为 “有 k_i 个相同的物品，每个物品只有一件”。这样就转换成了一个 01 背包模型，套用上文所述的方法就可已解决。

优化

二进制分组优化

int index = 0;
for (int i = 1; i <= m; i++)
{
	int c = 1, p, h, k;
  scanf ("%d%d%d", &p, &h, &k);
  while (k - c > 0)
  {
    k -= c;
    list[++index].w = c * p;
    list[index].v = c * h;
    c *= 2;
  }
  list[++index].w = p * k;
  list[index].v = h * k;
}

混合背包

简介

已知条件有第 i 个物品的重量 w[i]，价值 v[i]，以及背包的总容量 W。

特点

有多样物品

每样物品有 1 件 / k 件 或 无数件
每件物品只有 取 或 不取 两种状态

思路

将每一类背包问题分别求解

for (循环物品种类)
{
  if (是 01 背包)
    套用 01 背包代码;
  else if (是完全背包)
    套用完全背包代码;
  else if (是多重背包)
    套用多重背包代码;
}

二维费用背包

简介

已知条件有第 i 个物品的重量 w[i]，耗时 t[i]，价值 v[i]，以及背包的总容量 W。

特点

有多样物品

每样物品只有 1 件
每件物品只有 取 或 不取 两种状态

模板

for (int k = 1; k <= n; k++)	//对物品进行枚举
  for (int i = m; i >= mi; i--)	// 对经费进行一层枚举
    for (int j = t; j >= ti; j--)	// 对时间进行一层枚举
      dp[i][j] = max(dp[i][j], dp[i - mi][j - ti] + 1);

分组背包

简介

所谓分组背包，就是将物品分组，每组的物品 相互冲突 ，最多只能选一个物品放进去。

思路

从「在所有物品中选择一件」变成了「从当前组中选择一件」，于是就对每一组进行一次 01 背包就可以了。

可以将 t[k][i] 表示第 k 组的第 i 件物品的编号是多少，再用 cnt[k] 表示第 k 组物品有多少个。

模板

for (int k = 1; k <= ts; k++)          // 循环每一组
  for (int i = m; i >= 0; i--)         // 循环背包容量
    for (int j = 1; j <= cnt[k]; j++)  // 循环该组的每一个物品
      if (i >= w[t[k][j]])
        dp[i] = max(dp[i], dp[i - w[t[k][j]]] + c[t[k][j]]);  // 像0-1背包一样状态转移

注意循环顺序

有依赖的背包

简介

如果选第 i 件物品，就必须选第 j 件物品，保证不会循环引用，一部分题目甚至会出现多叉树的引用形式。为了方便，就称不依赖于别的物品的物品称为「主件」，依赖于某主件的物品称为「附件」。

思路

对于包含一个主件和若干个附件的集合有以下可能性：仅选择主件，选择主件后再选择一个附件，选择主件后再选择两个附件……需要将以上可能性的容量和价值转换成一件件物品。因为这几种可能性只能选一种，所以可以将这看成分组背包。

如果是多叉树的集合，则要先算子节点的集合，最后算父节点的集合。

区间DP

简介

区间类动态规划是线性动态规划的扩展，它在分阶段地划分问题时，与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系。令状态 f(i, j) 表示将下标位置 i 到 j 的所有元素合并能获得的价值的最大值，那么 f(i, j) = max { f(i, k) + f(k + 1, j) + cost }，cost 为将这两组元素合并起来的代价。

特点

合并：即将两个或多个部分进行整合，当然也可以反过来；
特征：能将问题分解为能两两合并的形式；
求解：对整个问题设最优值，枚举合并点，将问题分解为左右两个部分，最后合并两个部分的最优值得到原问题的最优值。

思路

既然让我求解在一个区间上的最优解，那么我把这个区间分割成一个个小区间，求解每个小区间的最优解，再合并小区间得到大区间即可。所以在代码实现上，我可以枚举区间长度 len 为每次分割成的小区间长度（由短到长不断合并），内层枚举该长度下可以的起点，自然终点也就明了了。然后在这个起点终点之间枚举分割点，求解这段小区间在某个分割点下的最优解。

模板

for(int len = 1; len <= n; len++)	//枚举长度
{
		for(int j = 1; j + len <= n + 1; j++)	//枚举起点，ends <= n
		{
				int ends = j + len - 1;
				for(int i = j; i < ends; i++)	//枚举分割点，更新小区间最优解
				{
					dp[j][ends] = min(dp[j][ends], dp[j][i] + dp[i+1][ends] + something);
				}
		}
}

朴素区间 DP O(n³)

Description

N 堆石子摆成一条线。现要将石子有次序地合并成一堆。规定每次只能选相邻的 2 堆石子合并成新的一堆，并将新的一堆石子数记为该次合并的代价。计算将 N 堆石子合并成一堆的最小代价。

Input

数据的第 1 行是正整数 N，表示有 N 堆石子。第 2 行有 N 个整数，第 i 个整数 a_i 表示第 i 堆石子的个数。

Output

输出共 1 行：最小得分。

Example Input

1
2

4
1 2 3 4

Example Output

Hint

1 2 3 4 (0) -> 3 3 4 (3) -> 6 4 (9) -> 10 (19)

Solution

f[x][y]：从 x 到 y 的最小得分

sum[x][y]：从 x 到 y 的重量和

转移方程：f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + sum[i][ends]);

其中 sum[x][y] 可以用前缀和数组 arr[] 代替，sum[x][y] = arr[y] - arr[x - 1]

Accepted Code

#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<iostream>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<list>
using namespace std;
#define INF 0x7fffffff

int n, a[101], arr[101];
int f[101][101];

int main()
{
    scanf ("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        scanf ("%d", &a[i]);
        arr[i] = arr[i-1] + a[i];
    }
    
    for (int p = 1; p < n; p++)
    {
        for (int i = 1, j = i + p; i < n && j <= n; i++, j = i + p)
        {
            f[i][j] = INF;
            for (int k = i; k < j; k++)
            {
                f[i][j] = min(f[i][j], f[i][k] + f[k+1][j] + arr[j] - arr[i-1]);
            }
        }
    }
    
    printf ("%d", f[1][n]);
    
    return 0;
  
}

线性变环状

Description

在一个圆形操场的四周摆放 N 堆石子，现要将石子有次序地合并成一堆。规定每次只能选相邻的 2 堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。试设计出一个算法，计算出将 N 堆石子合并成 1 堆的最小得分和最大得分。

Input

数据的第 1 行是正整数 N，表示有 N 堆石子。第 2 行有 N 个整数，第 i 个整数 a_i 表示第 i 堆石子的个数。

Output

输出共 2 行，第 1 行为最小得分，第 2 行为最大得分。

Example Input

1
2

4
4 5 9 4

Example Output

1
2

43
54

Hint

1 ≤ N ≤ 100，0 ≤ a_i ≤ 200 ≤ a_i ≤ 20。

Solution

f1[x][y]：从 x 到 y 的最小得分

sum[x][y]：从 x 到 y 的重量和

转移方程：f1[i][j] = min(f1[i][j], f1[i][k] + f1[k + 1][j] + sum[i][ends]);

其中 sum[x][y] 可以用前缀和数组 arr[] 代替 sum[x][y] = arr[y] - arr[x - 1]

Accepted Code

#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<iostream>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<list>
using namespace std;
#define INF 0x7fffffff

int n, minl, maxl, f1[300][300], f2[300][300], num[300];
int s[300];
int d(int i,int j)  //转移方程：f[i][j] = max(f[i][k]+f[k+1][j]+d[i][j];
{
    return s[j] - s[i - 1];
}

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n + n; i++) //因为是一个环，所以需要开到两倍再枚举分界线，最后肯定是最大的
    {
        scanf("%d", &num[i]);
        num[i + n] = num[i];
        s[i] = s[i - 1] + num[i];
    }
    for(int p = 1; p < n; p++)
    {
        for(int i = 1,j = i + p; (j < n + n) && (i < n + n); i++, j = i + p)
        {
            f2[i][j] = INF;
            for(int k = i; k < j; k++)
            {
                f1[i][j] = max(f1[i][j], f1[i][k] + f1[k + 1][j] + d(i, j));
                f2[i][j] = min(f2[i][j], f2[i][k] + f2[k + 1][j] + d(i, j));
            }
        }
    }
    minl = INF;
    for(int i = 1; i <= n; i++)
    {
        maxl = max(maxl, f1[i][i + n - 1]);
        minl = min(minl, f2[i][i + n - 1]);
    }
    
    printf("%d\n%d", minl, maxl);
    return 0;
}

四边形优化 O(n²)

思路

在查找最优分割点的时候，我们浪费了大量时间。那么我们可以把最优分割点保存下来，在查找的时候利用保存的最优分割点来优化查找过程。

四边形不等式优化

功能：用来寻找，s[i][j] （i ~ j 的最优分割点）与其他分割点的关系
不等式内容：如果某东西满足 a < b <= c < d 且f[a][c] + f[b][d] <= f[a][d] + f[b][c]，则说这个东西满足四边形不等式。简而言之：交叉小于包含！
结论关系：s[i][j-1] <= s[i][j] <= s[i+1][j]
证明过程：
1. 证明 w 满足四边形不等式，这里 w 是 m 的附属量，形如 m[i, j] = opt{ m[i, k] + m[k, j] + w[i, j] }，此时大多要先证明 w 满足条件才能进一步证明 m 满足条件
2. 证明 m 满足四边形不等式
3. 证明 s[i, j-1] ≤ s[i, j] ≤ s[i+1, j]

Code

#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<iostream>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<list>
using namespace std;
#define INF 0x7fffffff

int n;
int dp[2005][2005];
int sum[2005];
int relation[2005][2005];
int num[2005];

int main()
{
    scanf("%d", &n);
    memset(sum, 0, sizeof(sum));
    memset(dp, INF, sizeof(dp));
    for(int i = 1; i <= n; i++)
    {
        scanf("%d", &num[i]);
        dp[i][i] = 0;
        relation[i][i] = i;
        sum[i] = sum[i-1] + num[i];
    }
    for(int i = 1; i <= n; i++)
    {
        sum[i+n] = sum[i+n-1] + num[i];
        relation[i+n][i+n] = i + n; //分割点初始化
        dp[i+n][i+n] = 0;
    }
    for(int len = 1; len <= n; len++)
    {
        for(int j = 1; j + len <= 2 * n; j++)
        {
            int ends = j + len - 1;
            for(int k = relation[j][ends-1]; k <= relation[j+1][ends]; k++) //k的范围
            {
                if(dp[j][ends] > dp[j][k] + dp[k+1][ends] + sum[ends] - sum[j-1])
                {
                    dp[j][ends] = dp[j][k] + dp[k+1][ends] + sum[ends] - sum[j-1];
                    relation[j][ends] = k;
                }
            }
        }
    }
    int ans = INF;
    for(int i = 1; i <= n; i++)
    {
        ans = min(ans, dp[i][i+n-1]);
    }
    printf("%d\n", ans);
    
    return 0;
    
}

We give the following inductive definition of a “regular brackets” sequence:the empty sequence is a regular brackets sequence,if s is a regular brackets sequence, then (s) and [s] are regular brackets sequences, andif a and b are regular brackets sequences, then ab is a regular brackets sequence.no other sequence is a regular brackets sequenceFor instance, all of the following character sequences are regular brackets sequences: (), [], (()), ()[], ()[()] while the following character sequences are not: (, ], )(, ([)], ([(] Given a brackets sequence of characters a₁a₂ … a_n, your goal is to find the length of the longest regular brackets sequence that is a subsequence of s. That is, you wish to find the largest m such that for indices i₁, i₂, …, im where 1 ≤ i₁ < i₂ < … < i_m ≤ n, a_i1a_i2 … a_im is a regular brackets sequence.Given the initial sequence ([([]])], the longest regular brackets subsequence is [([])].

Input

The input test file will contain multiple test cases. Each input test case consists of a single line containing only the characters (, ), [, and ]; each input test will have length between 1 and 100, inclusive. The end-of-file is marked by a line containing the word “end” and should not be processed.

Output

For each input case, the program should print the length of the longest possible regular brackets subsequence on a single line.

Sample Input

((()))
()()()
([]])
)[)(
([][][)
end

Sample Output

Solution

题意：给出一个的只有 ‘(‘, ‘)’, ‘[‘, ‘]’ 四种括号组成的字符串，求最多有多少个括号满足题目里所描述的完全匹配。

动态转移方程：如果 s[i] 与 s[j] 匹配：dp[i][j] = dp[i+1][j-1] + 2

再遍历中间节点：dp[i][j] = max(dp[i][j], dp[i][k] + dp[k+1][j])

Accpted Code

#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<iostream>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<list>
using namespace std;
#define INF 0x7fffffff

char s[110];
int f[110][110];

int main()
{
    while (1)
    {
        memset (s, 0, sizeof (s));
        memset (f, 0, sizeof (f));
        scanf ("%s", s + 1);
        if (s[1] == 'e') return 0;
        s[0] = 1;
        int l = strlen (s+1);
        for (int p = 2; p <= l; p++)    //区间大小：2 ~ l
        {
            for (int i = 1, j = i + p - 1; j <= l; i++, j = i + p - 1)  //区间：i ~ j
            {
                if ((s[i] == '(' && s[j] == ')') || (s[i] == '[' && s[j] == ']'))
                    f[i][j] = f[i+1][j-1] + 2;
                for (int k = i; k < j; k++)
                {
                    f[i][j] = max(f[i][j], f[i][k] + f[k+1][j]);
                }
            }
        }
        
        printf ("%d\n", f[1][l]);
        
    }
    
    
    return 0;
    
}

POJ 1651 Multiplication Puzzle 抽卡片

Description

The multiplication puzzle is played with a row of cards, each containing a single positive integer. During the move player takes one card out of the row and scores the number of points equal to the product of the number on the card taken and the numbers on the cards on the left and on the right of it. It is not allowed to take out the first and the last card in the row. After the final move, only two cards are left in the row.

The goal is to take cards in such order as to minimize the total number of scored points.

For example, if cards in the row contain numbers 10 1 50 20 5, player might take a card with 1, then 20 and 50, scoring
10 * 1 * 50 + 50 * 20 * 5 + 10 * 50 * 5 = 500 + 5000 + 2500 = 8000
If he would take the cards in the opposite order, i.e. 50, then 20, then 1, the score would be
1 * 50 * 20 + 1 * 20 * 5 + 10 * 1 * 5 = 1000 + 100 + 50 = 1150.

Input

The first line of the input contains the number of cards N (3 <= N <= 100). The second line contains N integers in the range from 1 to 100, separated by spaces.

Output

Output must contain a single integer - the minimal score.

Sample Input

1 2	6 10 1 50 50 20 5

Sample Output

Solution

题意：给出 n 个数字，要求不能删除两端点的数字，然后删除其他数字的代价是该数字和左右相邻数字的乘积，问把数字（除端点）删完后的最小总代价。

dp[i][j]：抽出 i ~ (j - 1) 卡片的最小值

动态转移方程：dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j] + a[i-1] * a[k] * a[j])

Accepted Code

#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<iostream>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<list>
using namespace std;
#define INF 0x7fffffff

int n;
int a[101];
int dp[101][101];

int main()
{
    scanf ("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        scanf ("%d", &a[i]);
    }
    
    for (int p = 1; p < n; p++)
    {
        for (int i = 2, j = i + p; j <= n; i++, j = i + p)
        {
            dp[i][j] = INF;
            for (int k = i; k < j; k++)
            {
                dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j] + a[i-1] * a[k] * a[j]);
            }
        }
    }
    
    printf ("%d", dp[2][n]);
    
    
    return 0;
    
}

HDU 4632 Palindrome subsequence 最长回文子串

Description

In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements. For example, the sequence <A, B, D> is a subsequence of <A, B, C, D, E, F>.
http://en.wikipedia.org/wiki/Subsequence

Given a string S, your task is to find out how many different subsequence of S is palindrome. Note that for any two subsequence X = <S_x1, S_x2, …, S_xk> and Y = <S_y1, S_y2, …, S_yk> , if there exist an integer i (1 <= i <= k) such that xi != yi, the subsequence X and Y should be consider different even if S_xi = S_yi. Also two subsequences with different length should be considered different.

Input

The first line contains only one integer T (T <= 50), which is the number of test cases. Each test case contains a string S, the length of S is not greater than 1000 and only contains lowercase letters.

Output

For each test case, output the case number first, then output the number of different subsequence of the given string, the answer should be module 10007.

Sample Input

4
a
aaaaa
goodafternooneveryone
welcometoooxxourproblems

Sample Output

Case 1: 1
Case 2: 31
Case 3: 421
Case 4: 960

Solution

题意：给出一个字符串，求出其最多的可构成的回文字串（不要求连续），注：这里不同的回文字串只要求位置不同即可视为不同，如：aaaaa 的最多回文子串数目是 31.

dp[i][j]：i ~ j 构成的最多回文串个数

动态转移方程：

根据容斥定理：dp[i+1][j] 并 dp[i][j-1] = dp[i+1][j] + dp[i][j-1] - dp[i+1][j-1]
如果 s[i] == s[j]
- 两端单独可以构成回文子序列 + 1
- 与dp[i+1][j], dp[i][j-1], dp[i+1][j-1] 中的每个回文序列可以构成新的回文序列 + dp[i+1][j-1]

注：这里因为容斥时有减法，所以要先加上模再取模，否则会出现负数

dp[i][j] = (dp[i+1][j] + dp[i][j-1] - dp[i+1][j-1] + 10007) % 10007;

if (s[i] == s[j]) dp[i][j] = (dp[i][j] + dp[i+1][j-1] + 1) % 10007;

Accepted Code

#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<iostream>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<list>
using namespace std;
#define INF 0x7fffffff

int T;
char s[1010];
int dp[1010][1010];

int main()
{
    scanf ("%d", &T);
    for (int t = 1; t <= T; t++)
    {
        memset(s, 0, sizeof (s));
        memset(dp, 0, sizeof (dp));
        scanf ("%s", s + 1);
        int l = strlen(s + 1);
        for (int i = 1; i <= l; i++) dp[i][i] = 1;  //自己单独构成一个回文
        for (int p = 1; p <= l; p++)
        {
            for (int i = 1, j = i + p - 1; j <= l; i++, j = i + p - 1)
            {
                dp[i][j] = (dp[i+1][j] + dp[i][j-1] - dp[i+1][j-1] + 10007) % 10007;
                if (s[i] == s[j]) dp[i][j] = (dp[i][j] + dp[i+1][j-1] + 1) % 10007; //如果两端相等，dp[i][j] = 原来的 + 两端与中间每一个回文也可以构成回文（dp[i+1][j-1]) + 两端单独构成一个回文（1）
            }
        }
        printf ("Case %d: %d\n", t, dp[1][l]);
    }
    
    return 0;
    
}

DAG 上的 DP

简介

DAG 即 有向无环图，一些实际问题中的二元关系都可使用 DAG 来建模，如转化为 DAG 上的最长路、最短路和路径计数问题。

The Tower of Babylon

Descrpition

Perhaps you have heard of the legend of the Tower of Babylon. Nowadays many details of this tale have been forgotten. So now, in line with the educational nature of this contest, we will tell you the whole story:

The babylonians had n types of blocks, and an unlimited supply of blocks of each type. Each type-i block was a rectangular solid with linear dimensions (xi,yi,zi). A block could be reoriented so that any two of its three dimensions determined the dimensions of the base and the other dimension was the height.

They wanted to construct the tallest tower possible by stacking blocks. The problem was that, in building a tower, one block could only be placed on top of another block as long as the two base dimensions of the upper block were both strictly smaller than the corresponding base dimensions of the lower block. This meant, for example, that blocks oriented to have equal-sized bases couldn’t be stacked.

Your job is to write a program that determines the height of the tallest tower the babylonians can build with a given set of blocks.

Input

The input file will contain one or more test cases. The first line of each test case contains an integer n, representing the number of different blocks in the following data set. The maximum value for n is 30.

Each of the next n lines contains three integers representing the values xi, yi and zi. Input is terminated by a value of zero (0) for n.

Output

For each test case, print one line containing the case number (they are numbered sequentially starting from 1) and the height of the tallest possible tower in the format

‘Case case: maximum height = height’

Sample Input

Sample Output

Case 1: maximum height = 40
Case 2: maximum height = 21
Case 3: maximum height = 28
Case 4: maximum height = 342

Solution

建立 DAG

由于每个砖块的底面长宽分别严格小于它下方砖块的底面长宽，因此不难将这样一种关系作为建图的依据，而本题也就转化为最长路问题。

也就是说如果砖块 j 能放在砖块 i 上，那么 i 和 j 之间存在一条边 (i, j)，且边权就是砖块 j 所选取的高。

本题的另一个问题在于每个砖块的高有三种选法，怎样建图更合适呢？

不妨将每个砖块拆解为三种堆叠方式，即将一个砖块分解为三个砖块，每一个拆解得到的砖块都选取不同的高。

初始的起点是大地，大地的底面是无穷大的，则大地可达任意砖块，当然我们写程序时不必特意写上无穷大。

假设有两个砖块，三条边分别为 31, 41, 59 和 33, 83, 27，那么整张 DAG 应该如下图所示。

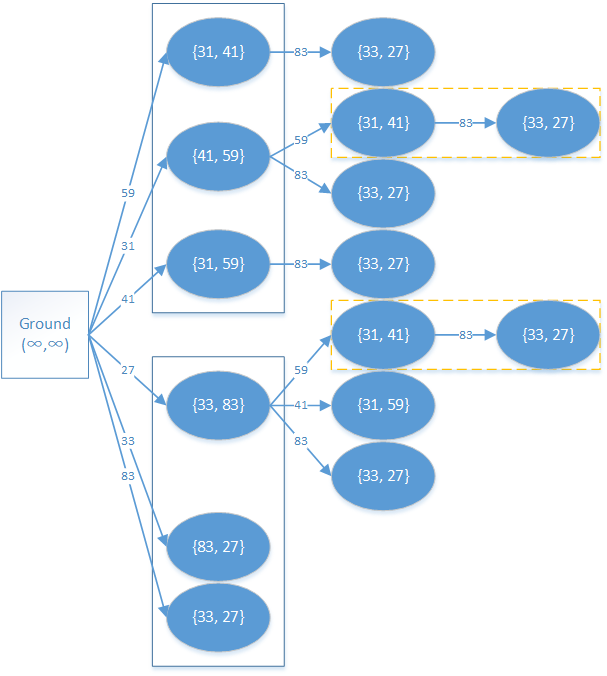
图中蓝实框所表示的是一个砖块拆解得到的一组砖块，之所以用 {} 表示底面边长，是因为砖块一旦选取了高，底面边长就是无序的。

图中黄虚框表示的是重复计算部分，为下文做铺垫。
转移

题目要求的是塔的最大高度，已经转化为最长路问题，其起点上文已指出是大地，那么终点呢？

显然终点已经自然确定，那就是某砖块上不能再搭别的砖块的时候。

之前在图上标记的黄虚框表明有重复计算，下面我们开始考虑转移方程。

显然，砖块一旦选取了高，那么这块砖块上最大能放的高度是确定的。

某个砖块 i 有三种堆叠方式分别记为 0, 1, 2，那么对于砖块 i 和其堆叠方式 r 来说则有如下转移方程 d(i, r) = max(d(j, r') + h')

其中 j 是所有那些在砖块 i 以 r 方式堆叠时可放上的砖块，r’ 对应 j 此时的摆放方式，也就确定了此时唯一的高度 h’。

在实际编写时，将所有 d(i, r) 都初始化为 -1，表示未计算过。

在试图计算前，如果发现已经计算过，直接返回保存的值；否则就按步计算，并保存。

最终答案是所有 d(i, r) 的最大值。

Accepted Code

#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<iostream>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<list>
using namespace std;
#define MAXN 35
#define MAXV 505

int t;
int d[MAXN][3];
int x[MAXN], y[MAXN], z[MAXN];

int babylon_sub(int c, int rot, int n)
{
    if (d[c][rot] != -1)
    {
        return d[c][rot];
    }
    d[c][rot] = 0;
    int base1 = 0, base2 = 0;
    if (rot == 0)
    {
        base1 = x[c];
        base2 = y[c];
    }
    if (rot == 1)
    {
        base1 = y[c];
        base2 = z[c];
    }
    if (rot == 2)
    {
        base1 = x[c];
        base2 = z[c];
    }
    for (int i = 0; i < n; i++)
    {
        if ((x[i] < base1 && y[i] < base2) || (y[i] < base1 && x[i] < base2))
            d[c][rot] = max(d[c][rot], babylon_sub(i, 0, n) + z[i]);
        if ((y[i] < base1 && z[i] < base2) || (z[i] < base1 && y[i] < base2))
            d[c][rot] = max(d[c][rot], babylon_sub(i, 1, n) + x[i]);
        if ((x[i] < base1 && z[i] < base2) || (z[i] < base1 && x[i] < base2))
            d[c][rot] = max(d[c][rot], babylon_sub(i, 2, n) + y[i]);
    }
    
    return d[c][rot];
}

int babylon(int n)
{
    for (int i = 0; i < n; i++)
    {
        d[i][0] = -1;
        d[i][1] = -1;
        d[i][2] = -1;
    }
    int r = 0;
    for (int i = 0; i < n; i++)
    {
        r = max(r, babylon_sub(i, 0, n) + z[i]);
        r = max(r, babylon_sub(i, 1, n) + x[i]);
        r = max(r, babylon_sub(i, 2, n) + y[i]);
    }
    
    return r;
}

int main()
{
    while (1)
    {
        int n;
        scanf ("%d", &n);
        if (!n) return 0;
        for (int i = 0; i < n; i++)
        {
            scanf ("%d%d%d", &x[i], &y[i], &z[i]);
        }
        printf ("Case %d: maximum height = %d\n", ++t, babylon(n));
    }
    
    return 0;
    
}

树形 DP

简介

树形 DP，即在树上进行的 DP。由于树固有的递归性质，树形 DP 一般都是递归进行的。

特点

不存在环
具有明显而又严格的层数关系

建树

如果节点数小于 5000，那么我们可以用邻接矩阵存储，如果更大可以用邻接表来存储（注意边要开到 2 * n，因为是双向的）。如果是二叉树或者是需要多叉转二叉，那么我们可以用两个一维数组 brother[], child[] 来存储

树形 DP 方程

通过观察孩子和父亲之间的关系建立方程。我们通常认为，树形DP的写法有两种：

根到叶子，不过这种动态规划在实际的问题中运用的不多。
叶子到根：即根的子节点传递有用的信息给根，完后根得出最优解的过程。这类的习题比较的多。

注：这两种写法一般情况下是不能相互转化的。但是有时可以同时使用

加分二叉树

Description

设一个 nn 个节点的二叉树 tree 的中序遍历为 (1, 2, 3, …, n)，其中数字 1, 2, 3, …, n 为节点编号。每个节点都有一个分数（均为正整数），记第 i 个节点的分数为 d_i，tree 及它的每个子树都有一个加分，任一棵子树 subtree（也包含 tree 本身）的加分计算方法如下：

subtree 的左子树的加分 × subtree 的右子树的加分 + subtree 的根的分数。

若某个子树为空，规定其加分为 1，叶子的加分就是叶节点本身的分数。不考虑它的空子树。

试求一棵符合中序遍历为 (1, 2, 3, …, n) 且加分最高的二叉树 tree。要求输出tree 的最高加分。tree 的前序遍历。

Input

第 1 行 1 个整数 n，为节点个数。

第 2 行 n 个用空格隔开的整数，为每个节点的分数

Output

第 1 行 1 个整数，为最高加分（ans ≤ 4,000,000,000）。

第 2 行 n 个用空格隔开的整数，为该树的前序遍历。

Sample Input

1 2	5 5 7 1 2 10

Sample Output

1 2	145 3 1 2 4 5

Hint

n < 30

分数 < 100

Solution

看到这个问题，我们首先应该想到的是这道题是否属于动态规划，而这里我们发现，结合问题，如果整棵树的权值最大，必然有左子树的权值最大，右子树的权值也最大，符合最优性原理。所以是动态规划。

而却不是一道树规的题目。因为我们可以用区间动规的模型解决掉：直接定义一个 f[i][j] 表示从 i 到 j 的最大值，则 f[i][j] = max(f[i][k-1] * f[k+1][j] + f[k][k])，枚举 k 即可。接下来是如何建树的问题，只有把树建好了，才能输出其前序遍历。于是，我们看到了两个关键词：二叉树，中序遍历。有了这两个关键词，加上区间动规，这棵树就能建起来了。根据二叉树的特性来建树。所以这颗树的前序遍历，只需要边动规边记录下 root[i][j] = k 表示 i 到 j 的根为 k 即可确定树的构造。

Accepted Code

#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<iostream>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<list>
using namespace std;

const int MAXN = 50;

long long n;
long long f[MAXN][MAXN], root[MAXN][MAXN];

void print(long long l, long long r)
{
    if (l > r)return;
    printf("%lld ", root[l][r]);
    if (l == r)return;
    print(l, root[l][r] - 1);
    print(root[l][r]+1,r);
}

int main()
{
    scanf("%lld", &n);
    for (int i = 1; i <= n; i++)
    {
        scanf("%lld", &f[i][i]);
        f[i][i-1] = 1;
        root[i][i] = i;
    }
    for (int len = 1; len < n; ++len)
    {
        for (int i = 1; i + len <= n; ++i)
        {
            int j = i + len;
            f[i][j] = f[i + 1][j] + f[i][i];    //默认它的左子树为空，如果有的话，这肯定不是最优解
            root[i][j] = i; //默认从起点选根
            for (int k = i + 1; k < j; ++k)
            {
                if (f[i][j] < f[i][k - 1] * f[k + 1][j] + f[k][k])
                {
                    f[i][j] = f[i][k - 1] * f[k + 1][j] + f[k][k];
                    root[i][j] = k;
                }
            }
        }
    }
    
    cout << f[1][n] << endl;
    print(1, n);
    
    
    return 0;

}

树上背包 · 选课

Description

在大学里每个学生，为了达到一定的学分，必须从很多课程里选择一些课程来学习，在课程里有些课程必须在某些课程之前学习，如高等数学总是在其它课程之前学习。现在有 N 门功课，每门课有个学分，每门课有一门或没有直接先修课（若课程 a 是课程 b 的先修课即只有学完了课程 a，才能学习课程 b）。一个学生要从这些课程里选择 M 门课程学习，问他能获得的最大学分是多少？

Input

第一行有两个整数 N , M 用空格隔开。(1 ≤ N ≤ 300, 1 ≤ M ≤ 300) 接下来的 N 行,第 I + 1 行包含两个整数 k_i 和 s_i, k_i 表示第I门课的直接先修课，s_i 表示第 I 门课的学分。若 k_i = 0 表示没有直接先修课（1 ≤ k_i ≤ N, 1 ≤ s_i ≤ 20）。

Output

只有一行，选 M 门课程的最大得分。

Sample Input

Sample Output

Solution

这道题的意思是每本书要想选择一门课，必须要先学会它的必修课，所以这就形成了一种依赖行为，即选择一门课必须要选择必修课。那么他又说要选择的价值最大，这就要用到树形背包的知识了。

树形背包的基本代码形式（即上面的树形背包类）

/*
设dp[i][j]表示选择以i为根的子树中j个节点。
u代表当前根节点，tot代表其选择的节点的总额。
*/
void dfs(int u,int tot)
{
	for(int i = head[x]; i; i = e[i].next)
	{
		int v = e[i].to;
		for(int k = 0; k < tot; k++)	//这里k从o开始到tot-1，因为v的子树可以选择的节点是u的子树的节点数减一
			dp[v][k] = dp[u][k] + val[u];
		dfs(v, tot - 1);
		for(int k = 1; k <= tot; k++)
			dp[u][k] = max(dp[u][k], dp[v][k-1]);	//这里是把子树的值赋给了根节点，因为u选择k个点v只能选择k-1个点。
	}
}

Accepted Code

#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<iostream>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<list>
using namespace std;

int n,m;

struct edge
{
    int next,to;
}e[1000];

int rt, head[1000], tot, val[1000], dp[1000][1000];

void add(int x,int y)
{
    e[++tot].next=head[x];
    head[x] = tot;
    e[tot].to = y;
}

void dfs(int u, int t)
{
    if (t <= 0) return;
    for (int i = head[u]; i; i = e[i].next)
    {
        int v = e[i].to;
        for (int k = 0; k < t; ++k)
            dp[v][k] = dp[u][k] + val[v];
        dfs(v, t - 1);
        for (int k = 1; k <= t; ++k)
            dp[u][k] = max(dp[u][k], dp[v][k-1]);
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)
    {
        int a;
        scanf("%d%d", &a, &val[i]);
        if(a)  add(a, i);
        if(!a) add(0, i);
    }
    
    dfs(0, m);
    
    printf("%d", dp[0][m]);
    
    return 0;
    
}

状压 DP

简介

状压 dp 是动态规划的一种，通过将状态压缩为整数来达到优化转移的目的。

互不侵犯

Descrpition

在 N × N 的棋盘里面放 K 个国王，使他们互不攻击，共有多少种摆放方案。国王能攻击到它上下左右，以及左上左下右上右下八个方向上附近的各一个格子，共 8 个格子。

Input

只有一行，包含两个数 N，K (1 <= N <=9, 0 <= K <= N * N)

Output

所得的方案数

Sample Input

3 2

Sample Output

Solution

首先，看到这一题，就知道如果不是搜索，就是 DP。当然搜索是过不了的，所以就应该尝试想出一个 DP 的解法。

DP 的前提之一当然是要找出一个可以互相递推的状态。显然，目前已使用的国王个数当然必须是状态中的一个部分，因为这是一个限制条件。那么除此之外另外的部分是什么呢？

我们考虑到每行每列之间都有互相的约束关系。因此，我们可以用行和列作为另一个状态的部分（矩阵状压 DP 常用行作为状态，一下的论述中也用行作为状态）。

又看到数据范围： 1 <= N <= 9。这里我们就可以用一个新的方法表示行和列的状态：数字。考虑任何一个十进制数都可以转化成一个二进制数，而一行的状态就可以表示成这样——例如：

1010 (2 进制)

就表示：这一行的第一个格子没有国王，第二个格子放了国王，第三个格子没有放国王，第四个格子放了国王（注意，格子从左到右的顺序是与二进制从左到右的顺序相反的，因为真正在程序进行处理的时候就像是这样的）。而这个二进制下的数就可以转化成十进制：

10 (10)

于是，我们的三个状态就有了：第几行（用 i 表示）、此行放什么状态（用 j 表示）、包括这一行已经使用了的国王数（用 s 表示）。

考虑状态转移方程。我们预先处理出每一个状态（sit[x]）其中包含二进制下 1 的个数，及此状态下这一行放的国王个数（gs[x]），于是就有：

f[i][j][s] = sum(f[i−1][k][s−gs[j]])，f[i][j][s] 就表示在只考虑前 i 行时，在前 i 行（包括第 i 行）有且仅有 s 个国王，且第 i 行国王的情况是编号为 j 的状态时情况的总数。而 k 就代表第 i - 1 行的国王情况的状态编号

其中 k 在 1 到 n 之间，j 与 k 都表示状态的编号，且 k 与 j 必须满足两行之间国王要满足的关系。（对于这一点的处理我们待会儿再说）

这个状态转移方程也十分好理解。其实就是上一行所有能够与这一行要使用的状态切合的状态都计入状态统计的加和当中。其中 i, j, s, k 都要枚举。

再考虑国王之间的关系该如何处理呢？在同一行国王之间的关系我们可以直接在预处理状态时舍去那些不符合题意的状态，而相邻行之间的关系我们就可以用到一个高端的东西：位运算。由于状态已经用数字表示了，因此我们可以用与（∧）运算来判断两个状态在同一个或者相邻位置是否都有国王——如果：

sit[j] & sit[k] (及上下有重复的king)

(sit[j] << 1) & sit[k] (及左上右下有重复king)

sit[j] & (sit[k]<<1) (及右上左下有重复king)

这样就可以处理掉那些不符合题意的状态了。

总结一下。其实状压 DP 不过就是将一个状态转化成一个数，然后用位运算进行状态的处理。理解了这一点，其实就跟普通的 DP 没有什么两样了。

Accepted Code

#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<iostream>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<list>
using namespace std;

int sit[2000], gs[2000];
int cnt = 0;
int n, yong;
long long f[10][2000][100], ans;

void dfs(int he, int sum, int node) //预处理出每一个状态
{
    if(node >= n)   //如果已经处理完毕（注意是大于等于）
    {
        sit[++cnt] = he;
        gs[cnt] = sum;
        return; //新建一个状态
    }
    
    dfs(he, sum, node + 1); //不用第node个
    dfs(he + (1 << node), sum + 1, node + 2);   //用第node个，此时node要加2，及跳过下一个格子
}

int main()
{
    scanf("%d%d", &n, &yong);
    dfs(0, 0, 0);
    for(int i = 1; i <= cnt; i++) f[1][i][gs[i]] = 1;   //第一层的所有状态均是有1种情况的
    for(int i = 2; i <= n; i++)
        for(int j = 1; j <= cnt; j++)
            for(int k = 1; k <= cnt; k++)   //枚举i、j、k
            {
                if(sit[j] & sit[k]) continue;
                if((sit[j] << 1) & sit[k]) continue;
                if(sit[j] & (sit[k] << 1)) continue;    //排除不合法国王情况
                for(int s = yong; s >= gs[j]; s--)  //枚举s，计算f[i][j][s]
                    f[i][j][s] += f[i-1][k][s-gs[j]];
            }
    
    for(int i = 1; i <= cnt; i++)
        ans += f[n][i][yong];   //统计最终答案，记得用long long
    printf("%lld", ans);
    
    return 0;
    
}

数位 DP

简介

数位 DP 问题往往都是这样的题型，给定一个闭区间 [l, r]，让你求这个区间中满足 某种条件 的数的总数。

数字计数

Description

给定两个正整数 a 和 b，求在 [a,b] 中的所有整数中，每个数码(digit)各出现了多少次。

Input

仅包含一行两个整数 a, b，含义如上所述。

Output

包含一行十个整数，分别表示 0∼9 在 [a,b] 中出现了多少次。

Sample Input

1 99

Sample Output

1	9 20 20 20 20 20 20 20 20 20

Hint

对于 30% 的数据，保证 a ≤ b ≤ 10⁶；
对于 100% 的数据，保证 1 ≤ a ≤ b ≤ 10¹²。

Solution

f[i] 代表在有i位数字的情况下，每个数字有多少个。如果不考虑前导 0，你会发现对于每一个数，它的数量都是相等的，也就是 f[i] = f[i-1] * 10 + 10^{i - 1};

我们先设数字为 ABCD

看 A000，如果我们要求出它所有数位之和，我们会怎么求？

鉴于我们其实已经求出了 0 ~ 9, 0 ~ 99, 0 ~ 999… 上所有数字个数（f[i], 且没有考虑前导 0）我们何不把这个 A000 看成 0000 ~ 1000 ~ 2000… A000 对于不考虑首位每一个式子的数字的出现个数为 A * f[3]。加上首位出现也就是小于 A 每一个数都出现了 10³ 次，再加上，我们就把 A000 处理完了。

这样你以为就把第一位处理完了？不不不，首位 A 还出现了 BCD + 1 次呢，也就是从 A000 ~ ABCD，这个 A 还出现了 BCD + 1 次，所以再加上这些才行呢。那么你发现，我们成功把首位代表的所有数字个数求出来了，剩下的求解与 A 完全没有任何关系，只是 BCD 的求解，于是我们发现我们已经把一个大问题，化成了一个个小问题，也即是，对于一个这样 n 位的数，把他一位位的分离开来。

当然你还需要处理前导 0 你会发现前导 0 一定是 0001, 0002, …, 0012, 0013, …, 0101, 0102, …, 0999 这样的数，一共出现了 10 *(i - 1) + 10 * (i - 2) + … 10 (i 表示数字位数），让 0 的统计减去这个值，那么恭喜你这道题做完了。

总结对于 DP 这个东西，最重要的其实只有一点，推状态，状态又是什么？是大问题的子问题，对于这种题最重要的特点是，无后效性，问题可拆分，并且答案的求解具有一定的规律，这样的题应该就可以用 DP 做，数位 DP 最重要的就是把一整个数字拆分成一位一位的单独来看，那么对于数位 DP，它的子问题也就一般是每一位上对于答案的求解，层层递进的这么一个思路。

Accepted Code

#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<iostream>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<list>
using namespace std;

long long a,b;
long long ten[20],f[20];
long long cnta[20],cntb[20];

void solve(long long x,long long *cnt)
{
    long long num[20]={0};
    int len=0;
    while(x)
    {
        num[++len]=x%10;
        x=x/10;
    }
    for(int i=len;i>=1;i--)
    {
        for(int j=0;j<=9;j++)
        cnt[j]+=f[i-1]*num[i];
        for(int j=0;j<num[i];j++)
        cnt[j]+=ten[i-1];
        long long num2=0;
        for(int j=i-1;j>=1;j--)
        {
            num2=num2*10+num[j];
        }
        cnt[num[i]]+=num2+1;
        cnt[0]-=ten[i-1];
    }
}

int main()
{
    scanf("%lld %lld",&a,&b);
    ten[0]=1;
    for(int i=1;i<=15;i++)
    {
        f[i]=f[i-1]*10+ten[i-1];
        ten[i]=10*ten[i-1];
    }
    solve(a-1,cnta);
    solve(b,cntb);
    for(int i=0;i<=9;i++)
    printf("%lld ",cntb[i]-cnta[i]);
}

About this Post

This post is written by OwlllOvO, licensed under CC BY-NC 4.0.

#C++#DP #区间DP

DP

DP

基础 DP

最长公共子串

特点

思路

模板

最长公共子序列

特点

模板

01 背包

简介

特点

思路

模板

优化

模板

完全背包

简介

特点

思路

模板

优化

模板

多重背包

简介

特点

思路

优化

二进制分组优化

混合背包

简介

特点

思路

二维费用背包

简介

特点

模板

分组背包

简介

思路

模板

有依赖的背包

简介

思路

区间DP

简介

特点

思路

模板

朴素区间 DP O(n3)

Description

Input

Output

Example Input

Example Output

Hint

Solution

Accepted Code

线性变环状

Description

Input

Output

Example Input

Example Output

Hint

Solution

Accepted Code

四边形优化 O(n2)

思路

四边形不等式优化

Code

Description

Input

Output

Sample Input

Sample Output

Solution

Accpted Code

Description

朴素区间 DP O(n³)

四边形优化 O(n²)